EX-A Spatial evaluation (optional / advanced)

This is an optional exercise intended for advanced course participants.

In the last session, you learned how to evaluate your species distribution model by separating the data into training, validation, and testing datasets. We did this by randomly splitting the data, a well-established method in machine learning. However, when working with spatial data, this method has limitations. Traditional validation approaches, such as random cross-validation, may not be suitable for SDMs due to spatial autocorrelation in the data.

Spatial autocorrelation

Spatial autocorrelation refers to the tendency of nearby locations to have similar environmental conditions. When spatial autocorrelation is present, data points close to each other are not truly independent, which can lead to inflated model performance estimates if not accounted for. Standard cross-validation approaches assume independence between training, validation, and testing data, which is often violated when data is separated randomly. Ignoring spatial autocorrelation can result in models that perform well in training but fail to generalize to new locations. Therefore, we need to account for spatial autocorrelation during model evaluation. Spatial validation techniques can help mitigate these biases by structuring data partitions in ways that reduce spatial dependence between training and testing sets. In spatial cross-validation the training, validation and test datasets get separated spatially instead of randomly. Which means points that are closer together in space will be in the same cross-validation fold. Several R packages, such as the blockCV package by Valavi et al. (2019), facilitate spatial cross-validation tasks. The figure below illustrates the difference between random and spatially separated folds.

Figure: (a) The presence-only and presence-absence datasets are clustered closely together, showing no spatial independence. (b) The presence-only data points are divided into spatial blocks, ensuring that the test dataset is spatially independent.

Spatial cross-validation techniques

To address spatial autocorrelation, various spatial cross-validation techniques have been developed. Several R packages, such as blockCV Valavi et al. (2019), ENMeval Kass et al. (2021), and CAST Meyer et al.(2025), offer implementations of these methods. Below, we introduce three commonly used spatial cross-validation approaches.

Spatial block cross-validation

In this approach, the study area is divided into spatial blocks, with the block size typically chosen by the user. The selection of block size can significantly influence model performance and evaluation outcomes.

The example below illustrates hexagons with a block size of 200 km for Pakistan, divided into seven spatial folds.

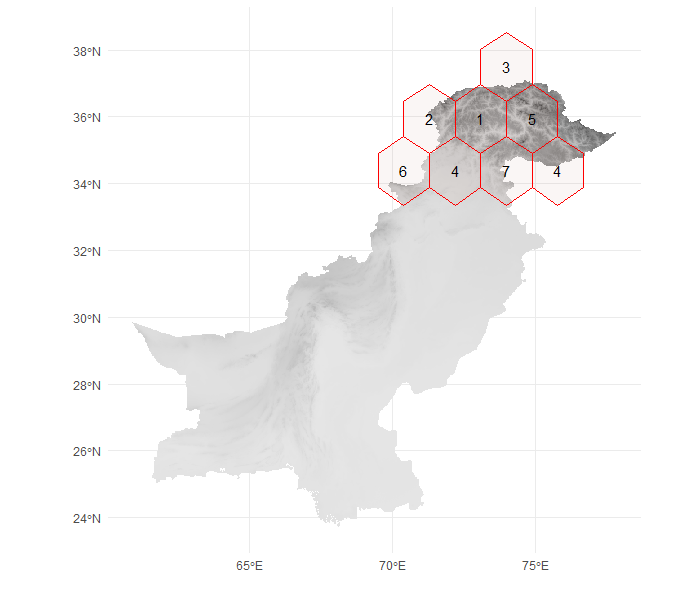
Checkerboard cross-validation

This method partitions the study area into a checkerboard pattern. By alternating inclusion and exclusion across the grid, this approach reduces spatial autocorrelation in model evaluation.

Image: Checkerboard separation from ENMeval 2.0.5 (Kass et al., 2025)

Spatial clustering cross-validation

Data points are grouped into spatial clusters, with entire clusters assigned to different folds. Clusters can be based on either the coordinates of occurrence points or spatial properties of environmental variables. If clustering is based on environmental variables, the process can become computationally intensive, especially when dealing with a large number of variables.

Spatial separation exercise

Previously we created the randomly separated testdataset with the following code:

`%not_in%`<- Negate(`%in%`)

testData=dplyr::slice_sample(Aglais_caschmirensis, prop=.15)
trainData=dplyr::filter(Aglais_caschmirensis, ID %not_in% testData$ID )

Now use the spatial_cv() function from the blockCV package to split your occxurence records. Into a training and test dataset:

folds= blockCV::cv_spatial(x=Aglais_caschmirensis,
                           r = r,
                           k = 7L,
                           hexagon = TRUE,
                           flat_top = FALSE,
                           size = 200000,
                           selection = "random",
                           iteration = 100L,)


Aglais_caschmirensis$folds <- folds$folds_ids

testData=Aglais_caschmirensis %>% dplyr::filter(folds %in% c(1,2))
trainData=Aglais_caschmirensis %>% dplyr::filter(folds %in% c(3,4,5,6,7) )


sf::write_sf(testData, "Aglais_caschmirensis_testData_spatial.gpkg")
sf::write_sf(trainData, "Aglais_caschmirensis_trainData_spatial.gpkg")```

Save the dataset for further usage. You will need it in your next assignment.